Summary

分类，是这类元件最早的用法。不过实际上，拿到一组数据，“分到什么类”和“该干什么事”其实是同一件事。
输入静态数据，输出静态结果，这本身就是一个自主决策过程，神经网络便是从此发育而来的。
如果输出的不是离散变量（类型A、类型B……）这其实也就是数据降维方法，有理想答案的，所以像是“这个元件负责对数据做出合理的概括”
关于计算机视觉入门 1）卷积分类器 - 编程中国的博客：卷积神经网络本身也包含全连接层用于分类；卷积层不是拿来分类或决策的，它只是一个过滤器，用于提取特征数据，输出是阵列，不能像传统分类器一样提取出一个单元。
我并不认为决策树值得单独拿出来作为一个模型。这只是一个中大规模模型的设计思想。

graph LR
s((Sense)) o--o C[Classifier] o--o d((Decision))

投票分类器

【总结】机器学习中的15种分类算法 - 知乎
 集成学习与随机森林（一）投票分类器 - ZacksTang - 博客园

我不认为随机森林值得单独拿出来作为一个模型。这只是一个中大规模模型的设计思想。

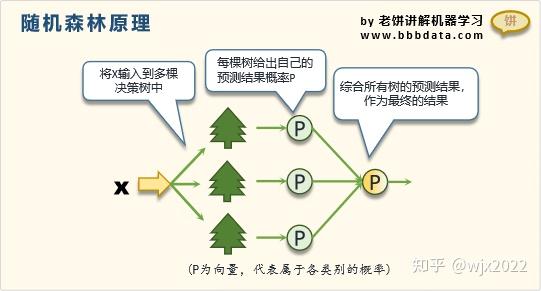
所谓随机森林，就是拿出多个决策树（森林），然后它们分类得到的结果不完全一致，则投票表决。推广来说，其实就是对不同结果的一个汇总器，汇总形式是投票。

基于近邻的方法

K近邻

一文搞懂k近邻（k-NN）算法（一） - 知乎

K值：寻找附近的K个邻近点。
邻近点中，少数服从多数，谁人多势众，新点就归谁

最近邻（K=1的K近邻）与Voronoi图

理解近似最近邻 (ANN) 问题中的图算法：Voronoi Diagram，Delaunay Graph，MSNET，RNG，MRNG和NSG - 知乎
K=1时，实际上就退化成“离谁近，就跟谁走”的ANN最近邻算法，那么不同阵营的点集就可以根据Voronoi图划界

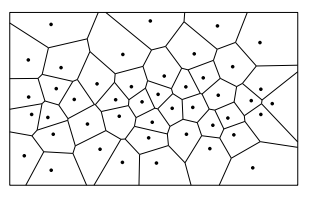
基于分割的方法

ID3、C4.5、C5.0

决策树之ID3算法详解(用于课堂展示)id3算法流程图-CSDN博客
决策树只是一种编程方式，这些算法只是根据信息熵来选择分割类型的维度（水平切一刀，再垂直切一刀……）

大津法（最大化类间方差法）

OTSU算法（大津法—最大类间方差法）原理及实现-CSDN博客
原本是对于图像像素的二分类算法，也就是图像分割。

基于权重的方法——从直线分割到神经元

感知机

【机器学习】感知机原理详解_感知机算法原理-CSDN博客
 一文彻底搞懂深度学习 - 感知机（perceptron） - Py学习
 什么是感知机？ - 知乎
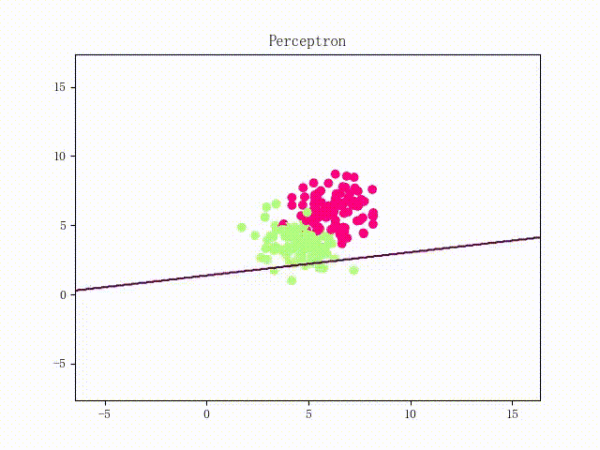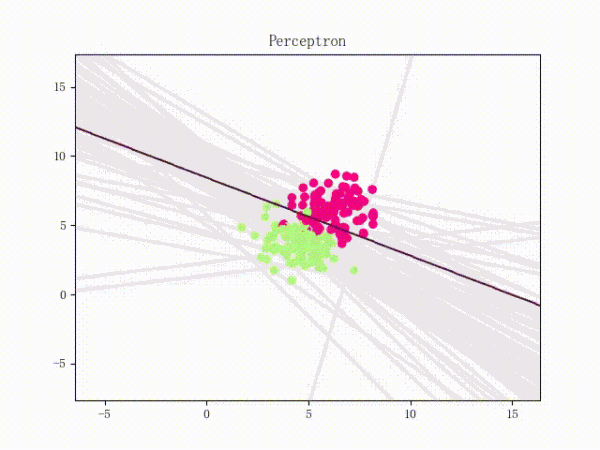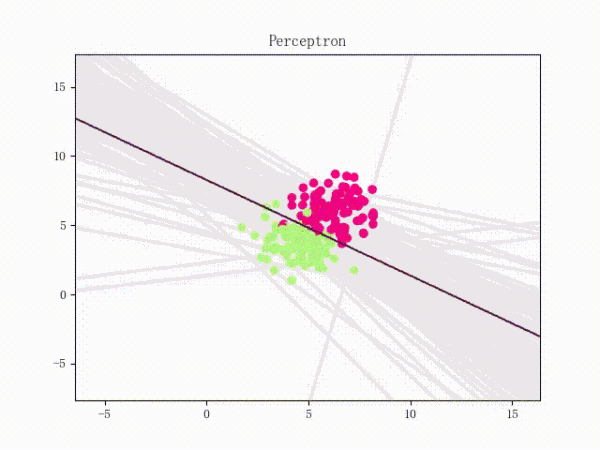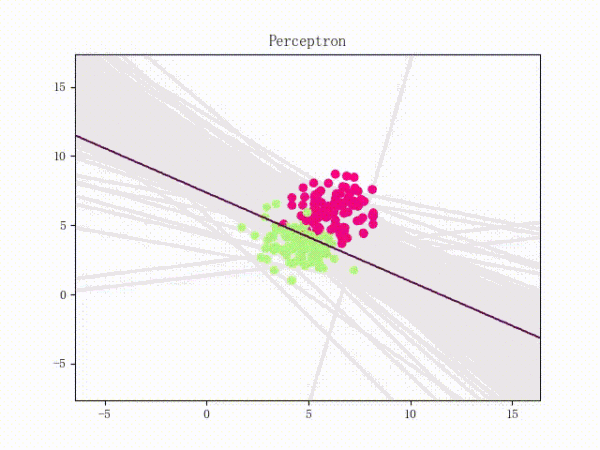
基于直线的分类方法（基于加权求和的分类方法，基于线性组合的分类方法）。是神经网络和支持向量机的基础。

f (x) = s i g n (\sum w_{i} \cdot x_{i} + b) (2.1)

sign是符号函数，其实也是一种阶跃函数（step function）

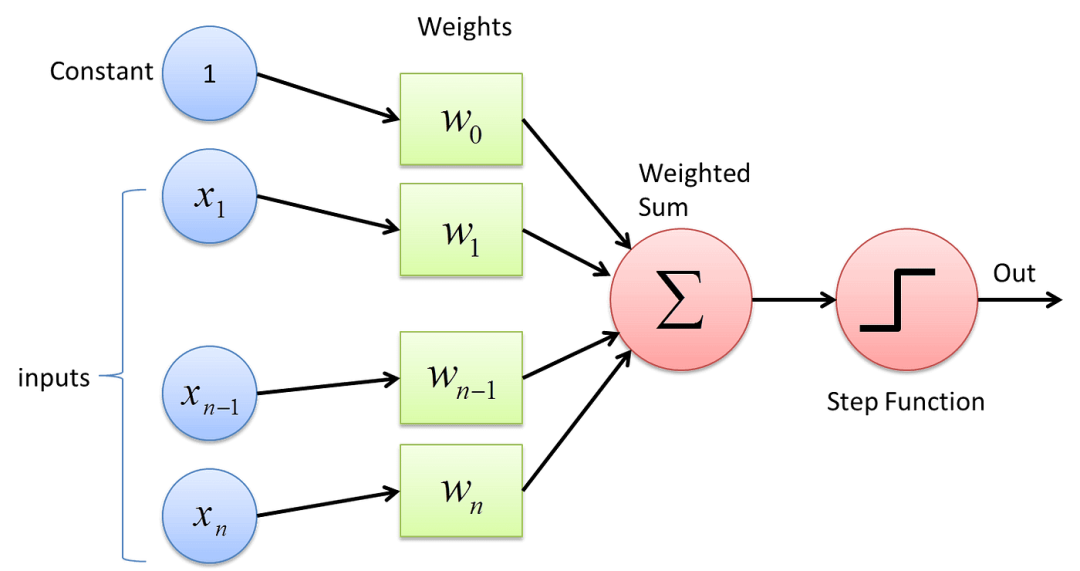
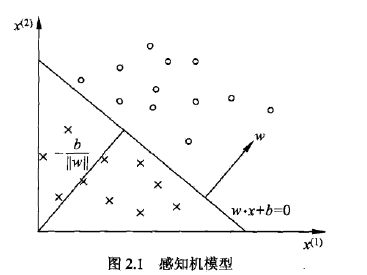
几何意义是基于直线的。我们知道 $\sum w_{i} \cdot x_{i} + b$ 和点到直线/平面/超平面的位置关系有关（和距离成正比），感知机就直接把空间中的数据点一分为二了。

参数整定目标：误分类点到超平面的总距离要小

需要确定的就是直线/平面/超平面方程的参数 $w$ 和 $b$ 。
损失函数（极小化的目标函数）：误分类点到超平面的总距离

d = \frac{| \vec{w} \cdot \vec{x} + b |}{| \vec{w} |} = - y \frac{\vec{w} \cdot \vec{x} + b}{| \vec{w} |}

把参数归一化（ $w$ 和 $b$ 等比例放缩，对直线/平面/超平面方程没有影响），设超平面S的误分类点集合为M，则损失函数为

L (w, b) = - \sum_{x_{i} ​ \in M} y_{i} ​ (\vec{w} \cdot \vec{x_{i}} ​ + b)

线性可分的感知机训练过程

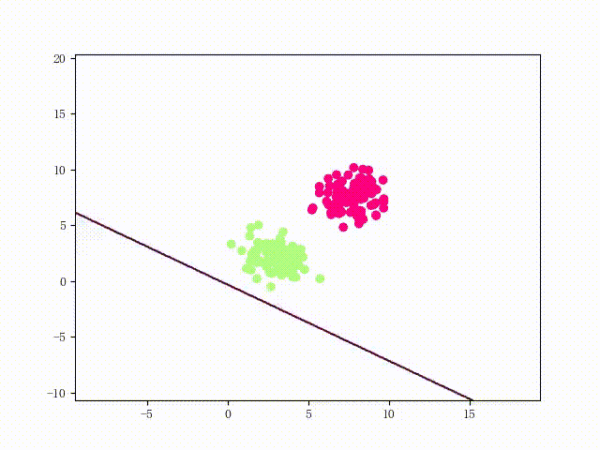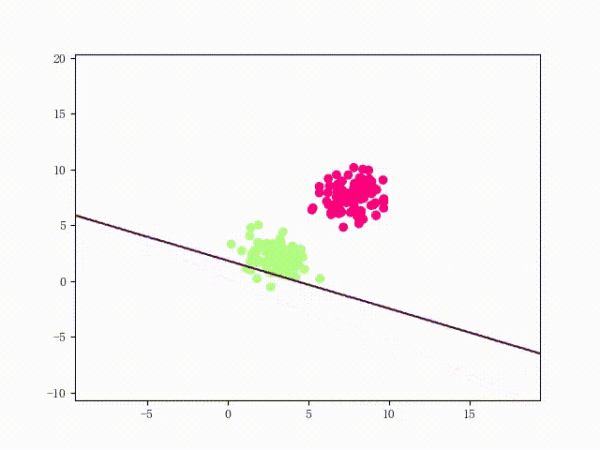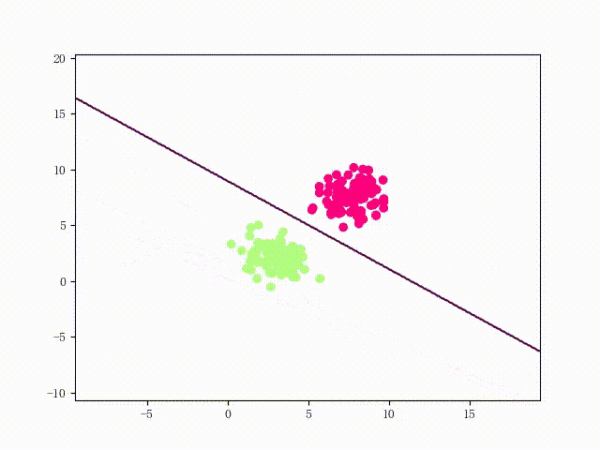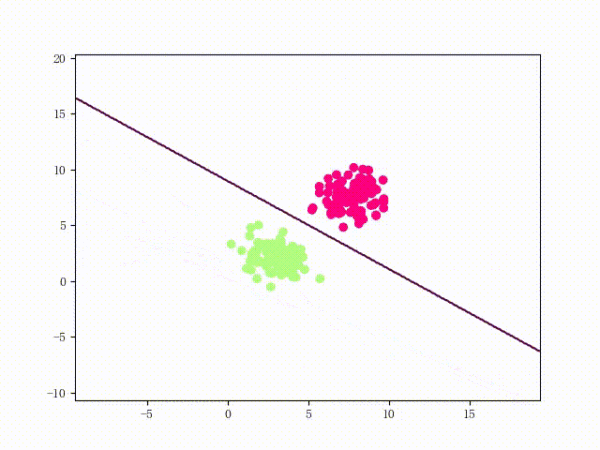
线性不可分的感知机训练过程

支持向量机

支持向量机（SVM）——原理篇
 支持向量机(SVM)原理详解 - 早起的小虫子 - 博客园
 感知机（perceptron）和支持向量机（svm）是一种东西吗？如果不是那他们的区别和关系是什么？ - 知乎
 感知机vs支持向量机 - Chen洋 - 博客园

基于直线的分类方法。同样是基于直线，与感知机的不同在于，要求点距离超平面几何间隔最大。
感知机目标找到一个超平面将各样本尽可能分离正确（有无数个）；
SVM目标找到一个超平面不仅将各样本尽可能分离正确，还要使各样本离超平面距离最远（只有一个），SVM的泛化能力更强

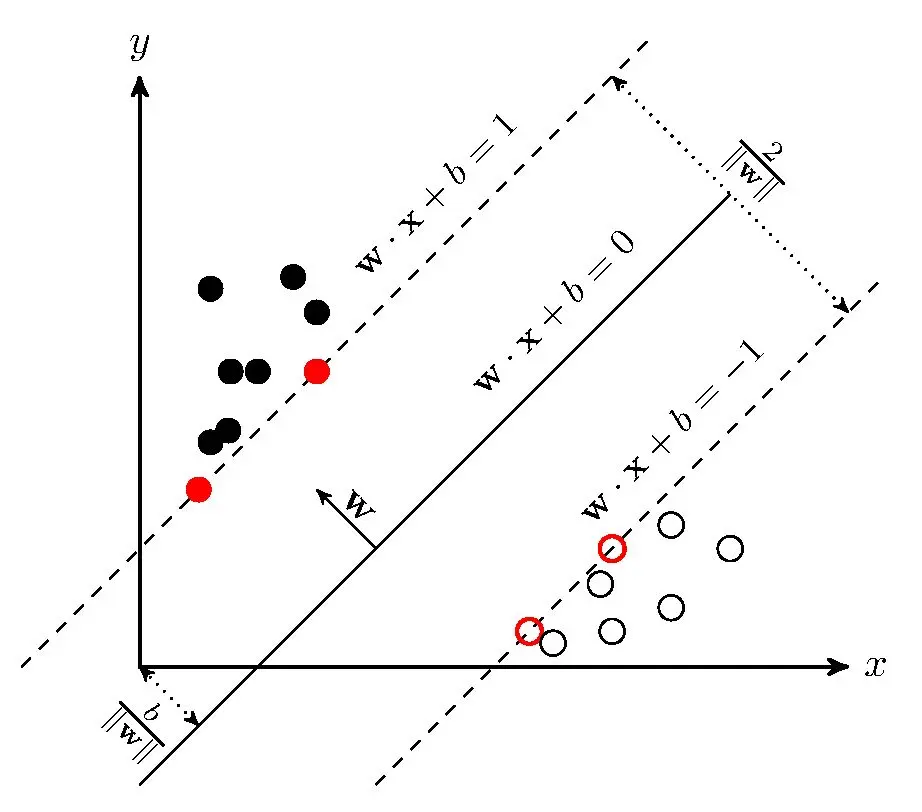
参数整定目标：最近点到超平面的最小距离要大

支持向量：离超平面最近的点的距离向量
参数归一化后，奖励函数

r e w a r d = min (y_{i} (\vec{w} \cdot \vec{x_{i}} + b))

另一种简化思路，令支持向量的 $\vec{w} \cdot \vec{x} + b = 1$ ，其他的就≥1了，因此上面的问题可以简化为：

Logistic回归——神经元

为什么说逻辑回归是单一神经元？ | MLOasis
一文带你从逻辑回归（Logistic）到神经网络（NN） - 知乎
 逻辑回归和神经网络之间有什么关系？逻辑回归和神经网络的关系-CSDN博客
 【机器学习】逻辑回归（非常详细） - 知乎
 逻辑回归（Logistic Regression)详解-CSDN博客
 逻辑回归（Logistic Regression） | 菜鸟教程
 游戏AI入门指南(Part 3) - 响应曲线 - LimboNova

为什么叫“回归”？

回归分析，可以解决“当新的因变量加入，自变量如何取值”
而逻辑回归，则把自变量编码成分类指标，解决的是“当新的数据点加入，类型分到哪一类”

基于直线的分类方法。但是从直接分类，多了一个激活函数。把sign函数换成了一个响应曲线——sigmoid函数（对数几率函数），输出的是分到某类的概率。
我们把类型编码为 $y \in {0, 1}$ ，则“输入某个数据点x的情况下，类型y为1的概率”是

P (y = 1 | x) = \hat{y} = s i g m o i d (w^{T} x + b) = \frac{1}{1 + e^{- (w^{T} x + b)}}

感知机、支持向量机，激活函数都是这样的

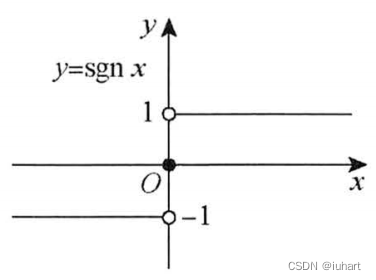
而逻辑回归让激活函数变平滑并赋予概率的意义（当然对于神经元，还有其他激活函数，如tanh、TeLU、ReLU等）

Question

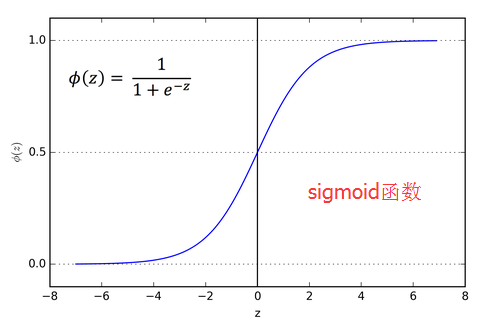
赋予概率的意义，这不就是策略网络么？

加上这个激活函数后看它的数据流结构，这明明就是一个使用sigmoid激活函数的神经元！

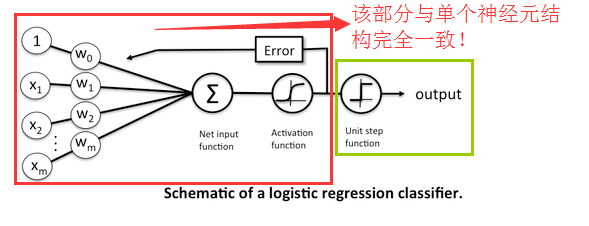
参数整定目标：已知点被分到正确类型的概率要大

极大似然估计：要让已知点被分到正确类型的概率 $\prod P (y | x)$ 最大化
为什么引入了指数？其实我们知道，这里y被编码成了0或1，这里指数的作用只是一个控制器，当y=1时 $\hat{y}$ 生效，当y=0时 $1 - \hat{y}$ 生效

P (y | x) = {\hat{y}}^{y} \cdot (1 - \hat{y})^{1 - y}

连乘，取对数，得奖励函数。前面添个负号，记 $\hat{y} = h_{θ} (x)$ ，得损失函数

\begin{array}{r} J (w, b) = - \frac{1}{m} \sum_{i = 1}^{m} [y^{(i)} \log (h_{θ} (x^{(i)})) + (1 - y^{(i)}) \log (1 - h_{θ} (x^{(i)}))] \end{array}

从神经元到神经网络

Softmax回归——单层神经网络

逻辑回归和神经网络之间有什么关系？逻辑回归和神经网络的关系-CSDN博客

其实，softmax regression可以看做是含有k个神经元的一层神经网络

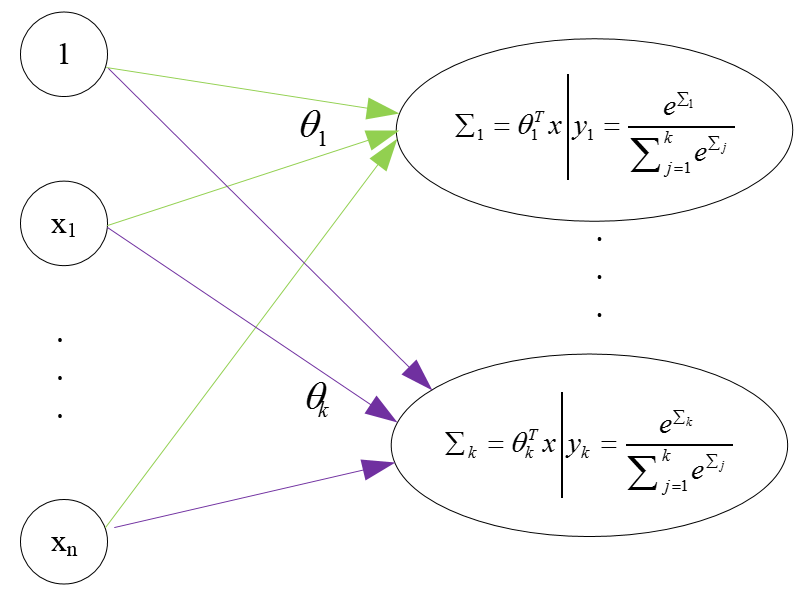
如果仅仅是要进行类别的预测，那么，只需要计算到sigma即可，不需要再求后面的softmax函数（上图所示的函数，注意，它与logistic regression中用到的sigmoid函数是不同的）
使用softmax函数，只是为了使输出具有概率意义，并且，有利于利用训练集去学习网络的权值；也可以这样理解，其实，softmax function只是在train的时候比较有用，利用它学习完网络参数后，在做predict的时候，其实就不需要它了（因为它是增函数）

神经网络全连接

深度学习之常用算子介绍_深度学习算子-CSDN博客
 多层感知机（MLP）、全连接神经网络（FCNN）、前馈神经网络（FNN）、深度神经网络（DNN）与BP算法详解_mlp和全连接层的区别-CSDN博客
 史上最全！27种神经网络简明图解：模型那么多，我该怎么选？-阿里云开发者社区
 什么是算子？ - 知乎

【机器学习】机器学习中的人工神经元模型有哪些？-阿里云开发者社区
 (47 封私信 / 6 条消息) 【深度学习基础】全连接层 (Fully Connected Layer) - 知乎
 对全连接层（fully connected layer）的通俗理解-腾讯云开发者社区-腾讯云
 一篇入门之-MLP多层感知机神经网络详细介绍及代码实现-老饼讲解
神经元：略
通用矩阵乘（GEMM）的具体应用。在图示中常常这样表示
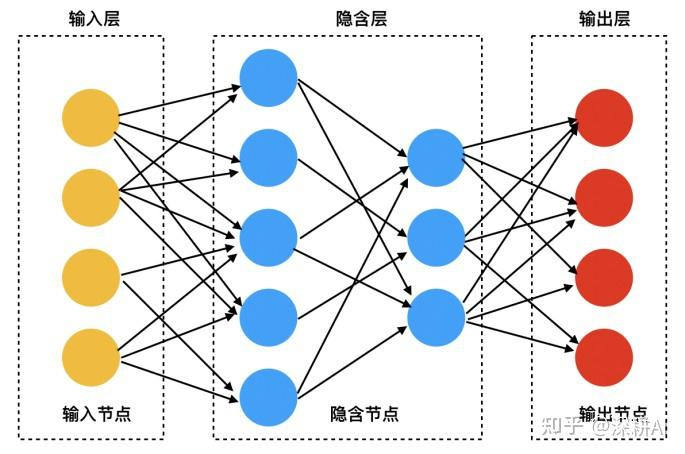
Pasted image 20250622041900.png
每个圆圈代表一个数，每个箭头代表把数倍增后加进新的数里面，俨然一个排列组合。

用矩阵乘法来表示

Success

这恰好就是图的“邻接矩阵”的概念

而我们表示排列组合，不光可以用多边形图形的方法表示，还可以用表格表示（就像比赛计分表一样）
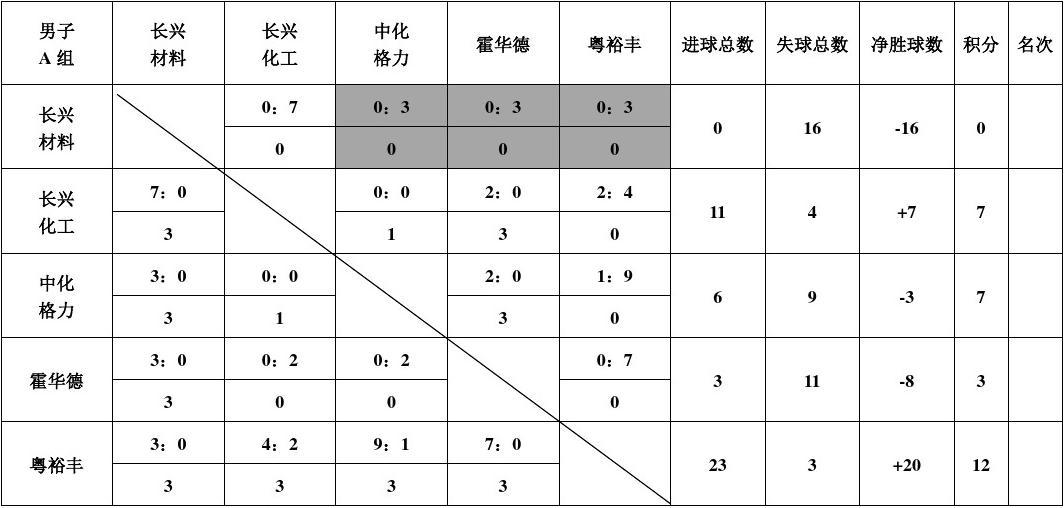
Pasted image 20250622042151.png
每个组合之间的倍数就写在表格中了，这恰恰可以用矩阵乘法表示。此外，引入偏置向量 $b$

y = A x + b

在这之后往往还会引入激活函数，于是就变成了

y = f (A x + b)

优化办法：反向传播（BP）算法、PPO算法……（Dropout：按概率关闭部分神经元，防止过拟合）

神经网络卷积层

卷积 Convolution 原理及可视化 - 知乎
 向量卷积的两种计算方法及符号向量的卷积-CSDN博客
 滑动窗口的卷积实现（Convolutional implementation of sliding windows）卷积的滑动窗口实现-CSDN博客
 [译文] 为什么GEMM是深度学习的核心 | Why GEMM is at the heart of deep learning - 简书
 卷积神经网络在分类层用卷积层代替全连接层的好处（附代码演示）卷积代替全连接做分类-CSDN博客

我们前面的基于权重的分类器，加权求和可以视为两个向量求点积
现在复习一下卷积：点积的变种。
原点处（向量首项）点积是一一对应乘，但定点处（向量某项）卷积是翻转后一一对应乘。
各个点的点积组成点积变换的函数，就是函数滑动取点积的结果
各个点的点积组成卷积变换的函数，就是函数滑动取卷积的结果

不过

对于点积，我们往往单独取出某个滑动位置的数值进行研究
对于卷积，我们往往整体考虑不同滑动位置的序列进行研究
所以
对于全连接层，有神经元作为基本单元
对于卷积层，我们不考虑其基本单元（那和翻转权重后的神经元有什么区别嘛）

用矩阵乘法来表示

讨论如何用矩阵乘法来表示卷积运算的。
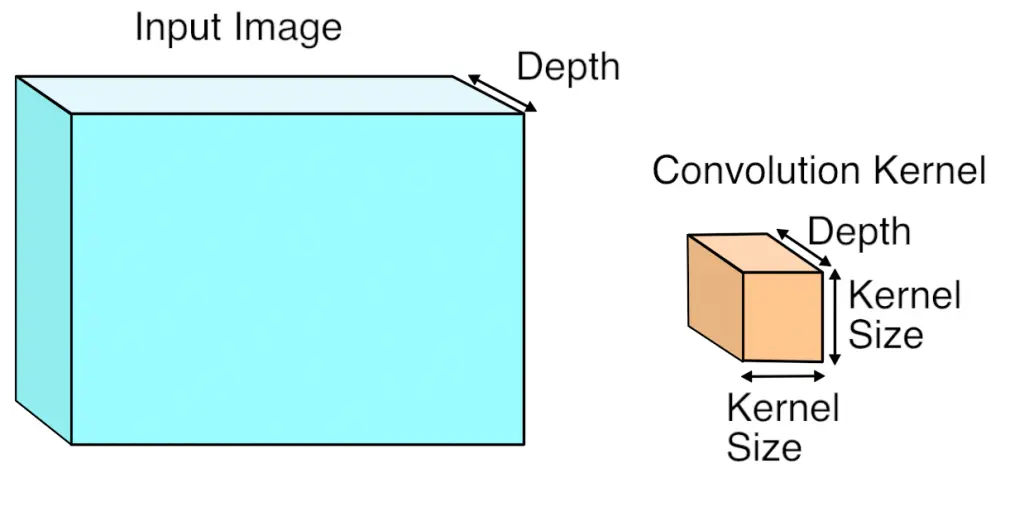
Pasted image 20250622164912.png
第一步是将输入图像（实际上是3D数组）转换为2D数组，我们可以将其视为矩阵。应用每个卷积核的地方是图像中的一个小三维立方体，因此我们将每个输入值立方体作为一列复制到矩阵中。这被称为im2col，即：image-to-column（图像到列），我相信它来自一个原始的Matlab函数，以下是将im2col可视化：

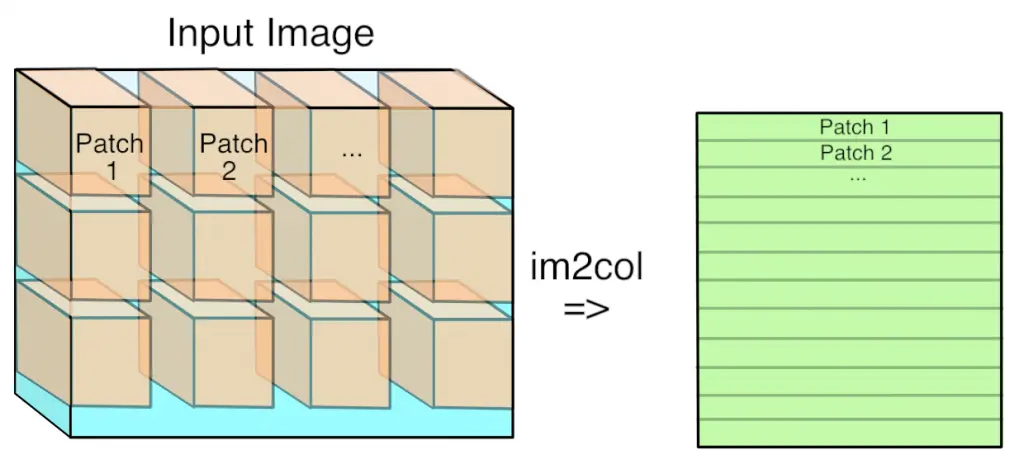
Pasted image 20250622164838.png

现在，如果你像我一样是对图像处理感兴趣的极客，你可能会对进行这种转换时，如果stride小于卷积核大小，所需内存的增加感到震惊。这意味着包含在重叠卷积核中的像素将在矩阵中进行复制，这似乎效率低下。不过，你必须相信我，这种内存使用的浪费会带来计算上的优势。

现在你有了矩阵形式的输入图像，你对每个卷积核的权重做了同样的操作，将3D立方体序列化成行，作为矩阵乘法的第二个矩阵。以下是最终GEMM的样子：

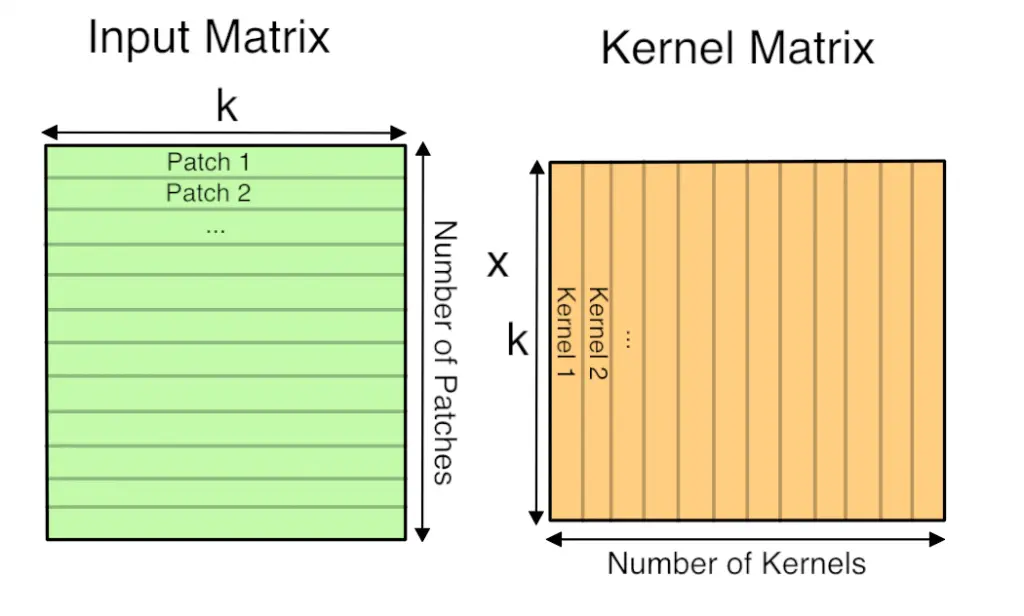
Pasted image 20250622164849.png

这里的“k”是每个patch和卷积核中的值的个数，所以它是卷积核宽度_高度_深度。得到的矩阵列高为“patch数”，行宽为“卷积数”。通过后续操作，该矩阵实际上被视为一个3D数组，方法是以核数维度作为深度，然后根据patch在输入图像中的原始位置将patch拆分回行和列。

基于概率的方法

朴素贝叶斯

【总结】机器学习中的15种分类算法 - 知乎

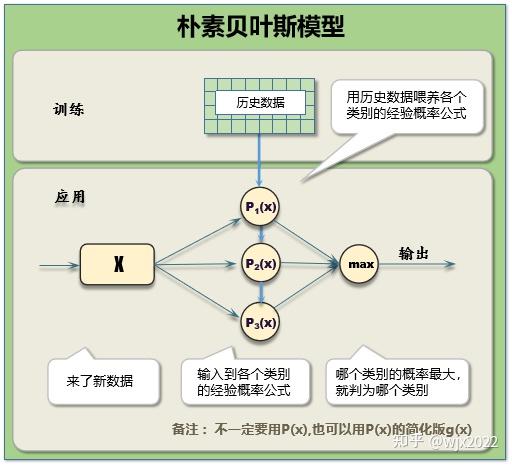
现有数据：数据。待估计量：类别。

离散情况

3分钟理解朴素贝叶斯（下） #AI #机器学习 #深度学习 #贝叶斯定理 #朴素贝叶斯 - 抖音
例子：买西瓜。可以看到下面的变量，都是离散变量

计算联合概率 $P (瓜熟, 脱落, 圆形, 青色)$
计算联合概率 $P (瓜生, 脱落, 圆形, 青色)$
计算后验概率 $P (瓜熟 | 脱落, 圆形, 青色)$ 和 $P (瓜生 | 脱落, 圆形, 青色)$

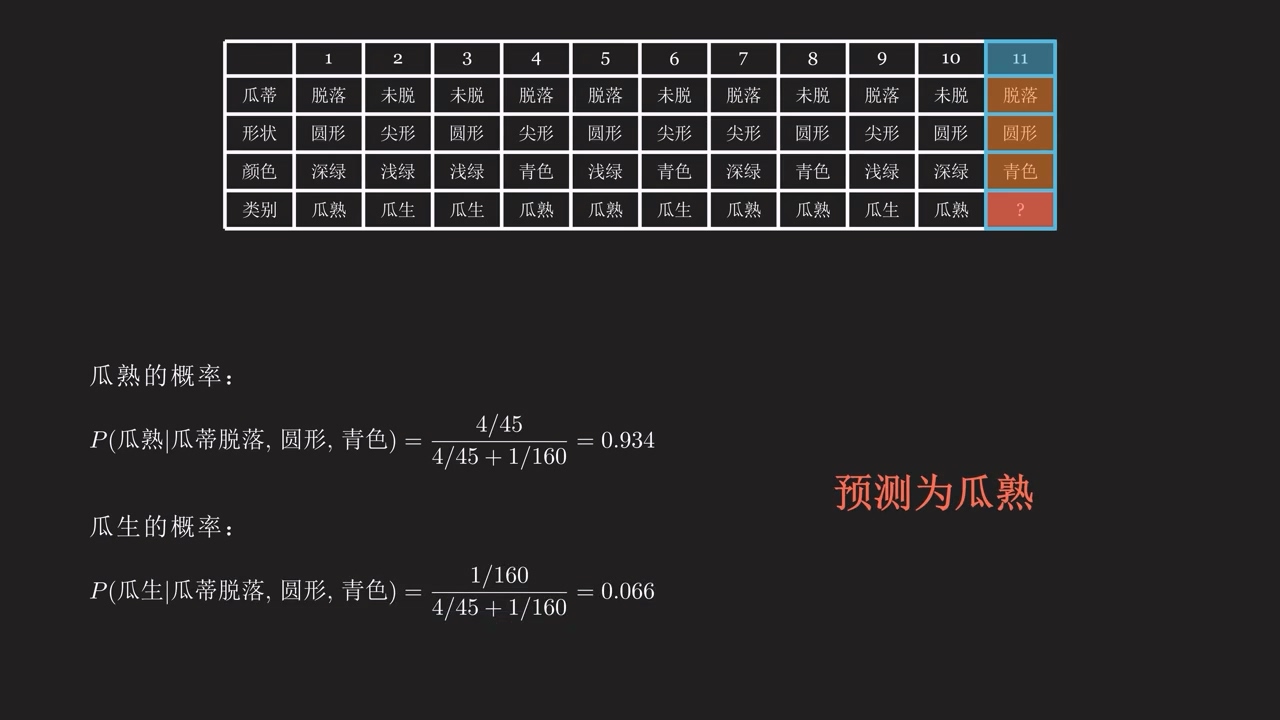
连续情况

从零开始实现朴素贝叶斯分类算法(连续特征情形) - 知乎
 朴素贝叶斯中 - 连续型特征属性和零概率事件处理 - 澄轶 - 博客园
 朴素贝叶斯法 - Milkha - 博客园

对于每一个属性，如果是连续数值，那么我们计算的其实不是概率，而是概率分布函数。
区间计算：把样本分段，计算各个段的概率，把概率分布函数构建为概率分布直方图。也可以再用概率分布曲线来拟合这个直方图。
假设分布：对于小样本，假设其服从某个分布，然后根据统计学量（均值、方差）来确定这个分布的各个系数。（有点像卡尔曼滤波用的方法）

Question

蒙特卡洛：或许可以不计算分布函数，用分布本身来替代分布函数？（灵感来自粒子滤波用的方法）这样或许可以大大减少计算时间，贝叶斯神经网络/量子神经网络，指日可待

知道概率分布函数后，对于新来的连续数值，我们也能计算其联合概率密度
进一步计算似然概率密度
- 对于一般的分类（二分类、多分类），输出离散值，我们需要先把似然概率密度积分（化成概率分布直方图）再比较，选择最可能的区间。
- 对于需要连续输出的情况（例如神经网络），我们可以按期望估计（后验期望估计），或者取概率密度最大值（最大后验概率估计）

代码
MachineLearning/Articles/机器学习010-用朴素贝叶斯分类器解决多分类问题.md at master · RayDean/MachineLearning
【火炉炼AI】机器学习010-用朴素贝叶斯分类器解决多分类问题前面讲到了使用逻辑回归分类器解决多分类问题（【火炉炼AI】 - 掘金

贝叶斯网络

【总结】机器学习中的15种分类算法 - 知乎
 【机器学习】朴素贝叶斯 -> 半朴素贝叶斯 -> 贝叶斯网络 -> 贝叶斯优化，看这一篇就够了！ - 知乎
 超详细讲解贝叶斯网络(Bayesian network) - USTC丶ZCC - 博客园

一次性弄懂马尔可夫模型、隐马尔可夫模型、马尔可夫网络和条件随机场！(词性标注代码实现) - mantch - 博客园
 游戏AI入门指南(Part 3) - LimboNova
游戏开发中的人工智能（十三）：不确定状态下的决策：贝叶斯技术_贝叶斯网络通常使用的三种推理是-CSDN博客
 贝叶斯网络、马尔可夫模型、马尔可夫过程、马尔可夫链、马尔可夫网络基本概念_马尔科夫链马尔科夫毯-CSDN博客
 游戏开发中的人工智能（十三）：不确定状态下的决策：贝叶斯技术_贝叶斯网络通常使用的三种推理是-CSDN博客
 超详细讲解贝叶斯网络(Bayesian network) - USTC丶ZCC - 博客园
 Causal Models（因果模型） - 知乎

若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。

例如，下面是朴素贝叶斯和半朴素贝叶斯分类器的贝叶斯网络表示

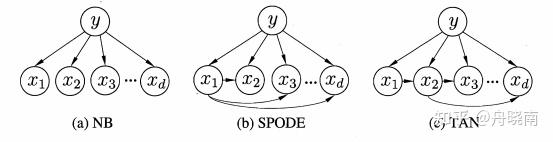
(a) 朴素贝叶斯，(b) 超父独依赖估计，(c) 树增广朴素贝叶斯

贝叶斯网络给出了不同指标的依赖关系，就可以根据历史数据训练出依赖关系之间的转移概率，就可以算出某个节点的概率公式。我要说：其实就是给出了策略网络。

Note

这里只是讲述其在分类器中的作用，其实这本身在状态转移的建模中也很有用

相比于朴素贝叶斯

联合概率的计算过程就变了，要根据概率图的实际情况来计算。
不同结果下的似然概率，还是可以根据联合概率算出的。
最后的估计，也是自己选择。离散的分类一般是最大似然估计，连续的输出一般是后验期望估计。

马尔可夫决策过程与策略网络

马尔科夫决策过程（Markov Decision Process, MDP） - 知乎
引入π函数，一个概率密度函数。最终的动作一般根据policy函数随机抽样得到，而不是人为指定控制逻辑。所以，输入的是状态，输出的是行动发生的概率。