graph LR
t((Target)) --> M[MotionCard] --> i((Interpolation))

如何对高维数据进行插值运算？ - 知乎
数学建模学习笔记 | 插值算法_多维插值算法-CSDN博客
【轨迹生成】曲线插值法_插值曲线矢量-CSDN博客
机器人的规划算法（一）——关节空间路径/轨迹规划算法 - 知乎
(48 封私信 / 60 条消息) 技术分享 | 李群与轨迹规划​ - 知乎
常见插值算法 | 计算机图形学笔记
数学建模笔记——插值拟合模型（一） - 简书
机器人的运动“规划”是给了路径点的，其实是拟合插值。

线性插值

略

梯形速度插值

其实就是匀加速运动起步，一段时间后匀速运动，快到终点匀减速运动刹车

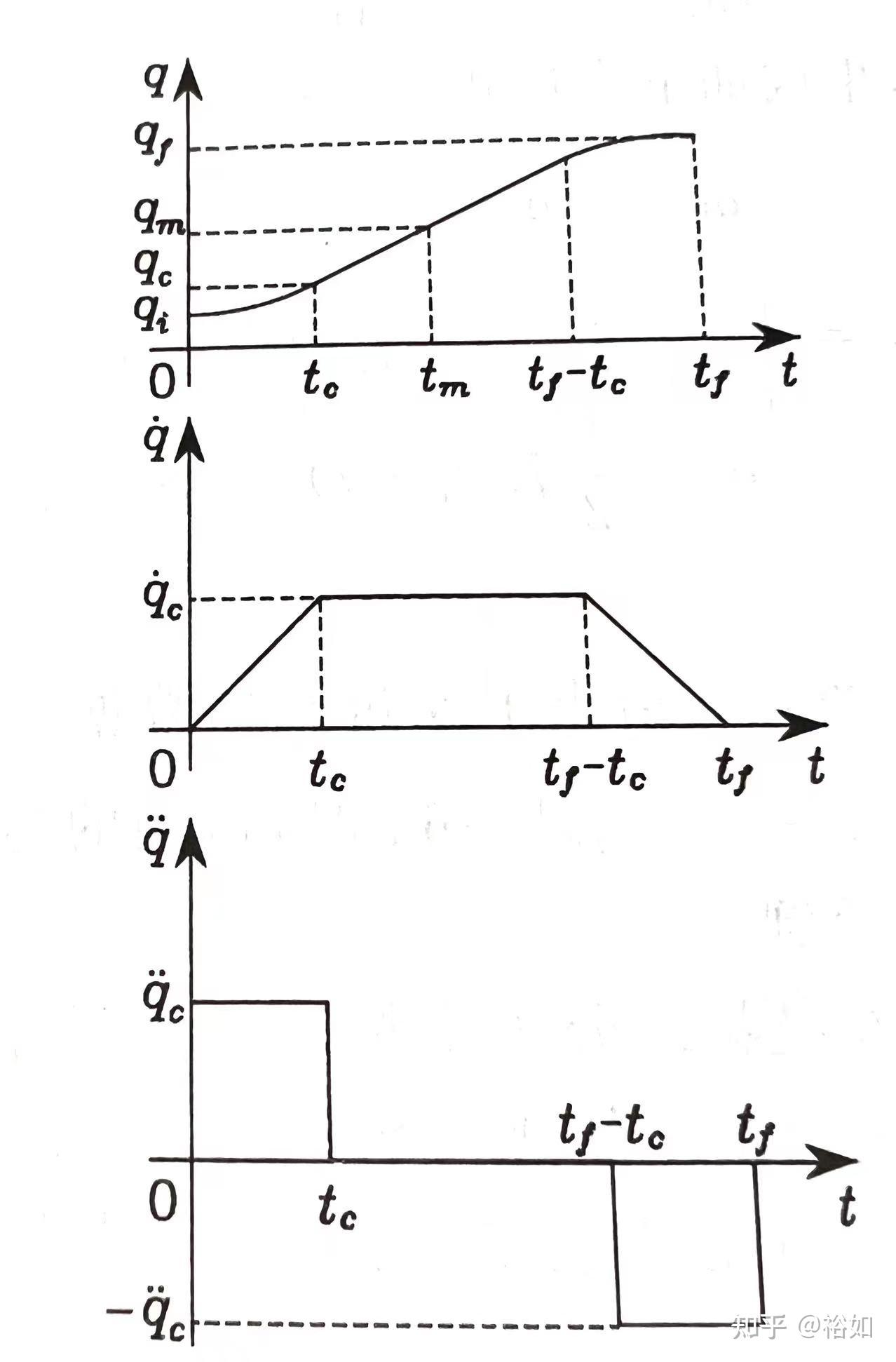
S形速度插值

运动控制——S型速度规划（一） - 知乎
一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）_s型速度曲线-CSDN博客

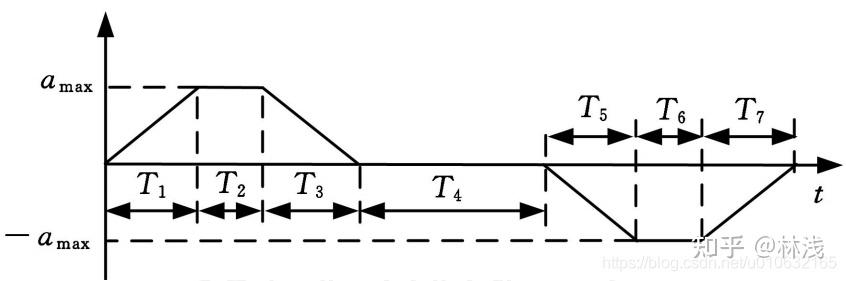
三角函数速度插值

数字信号处理 - -三角插值
ActionFZY给我的"腿规划"，好像就是这种规划
实际上还是曲线的拼接。速度-时间曲线的S形曲线变成了三角函数曲线

%% 定义速度-时间曲线
% 加速阶段: V(t) = v - v * cos(pi * t / accel_time)
accel_idx = t <= accel_time;
V(accel_idx) = v - v * cos(pi * t(accel_idx) / accel_time);

% 减速阶段: V(t) = Vmax - v * (1 - cos(pi * (t - accel_time) / decel_time))
decel_idx = t > accel_time;
t_decel_phase = t(decel_idx) - accel_time; % 减速段相对时间
V(decel_idx) = Vmax - v * (1 - cos(pi * t_decel_phase / decel_time)); % 调整公式

多项式插值

B样条（B-Splines) | Zhe Li
【数值分析】插值法之多项式插值（1）：拉格朗日法的算法介绍及代码实现（Python版） - 知乎
当时为了完成数学建模校赛，误打误撞推导出了拉格朗日插值法。

Akima插值

Makima插值

贝塞尔曲线

从零开始学图形学：10分钟看懂贝塞尔曲线 - 知乎
贝塞尔曲线与B样条 - 知乎
三阶（三个控制点）

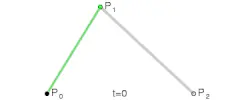
四阶（四个控制点）

五阶（五个控制点）

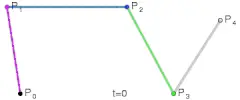
对于三阶贝塞尔曲线，点在动线段上，可以用$\overrightarrow{c}=(1-t)\overrightarrow{a}+t\overrightarrow{b}$来表示。如果你把整个递归的每一步都按这个展开，那么最终可以得到如下公式（伯恩斯坦形式）：

分段贝塞尔曲线

一旦确定了特征多边形的顶点数，就决定了曲线的阶数。如果曲线的阶数过高：

• 调整控制点对曲线的影响就比较小，调整起来相当麻烦。
• 数据点的数量太多，计算量急剧增加。
• 一条贝塞尔曲线无法做局部修改，牵一发而动全身。
  
  
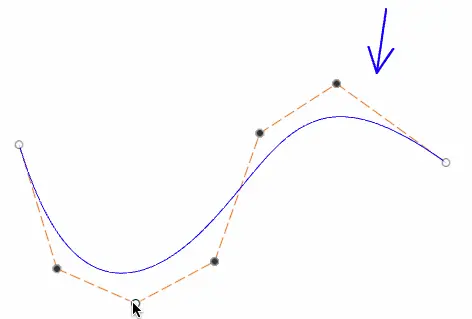
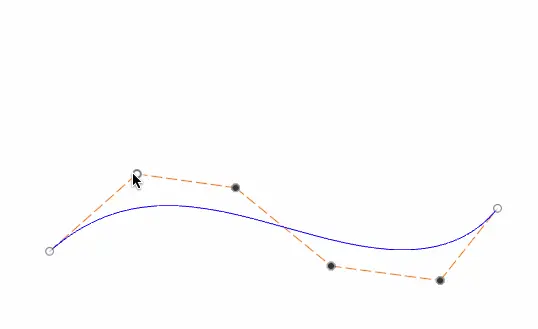
  于是常用的，是分段贝塞尔曲线
  对两侧的贝塞尔曲线求导，分别代入 t=0 和 t=1 （即贝塞尔曲线的开始和结束时间），让二者相等。此时能发现，当两侧控制点与分段交接点共线且形成的线段长度相等时，满足曲线平滑性质。
  
  再分享一个网站，可以在线玩贝塞尔曲线：Bezier Curve Edit

B样条

贝塞尔曲线与B样条 - 知乎
B样条（B-Splines) | Zhe Li

NURBS